اگر به تاریخ آفریقا نگاه کنیم،
قدیمیترین شئ ریاضی از 35000 سال پیش از میلاد در سوازیلند کشف شده.
قدیمیترین مثال حساب از 6000 سال پیش از میلاد در زئیر کشف شده.
هرم عظیم گیزا که یک شاهکار مهندسی است، حوالی سال 2650 پیش از میلاد در مصر ساخته شده.
پاپیروس مصری 4000 ساله معروف به مسکو، حاوی مطالبی از هندسه است.
لازم به اشاره است که، یونانیان نیز مبانی ریاضی را از بابلیان به ارث بردهاند.
ریاضیات مدون در حدود 2000 سال قبل از میلاد مسیح ، توسط بابلیان بوجود آمد .
در آن زمان بابلیان نتایج جبر مقدماتی را یکجا جمع کردند.
اما ریاضیات به مفهوم واقعی و امروزی آن ، در سرزمین یونان و در قرنهای 4 و 5 قبل از میلاد ایجاد شد.
به تدریج توسعه یافت، اوج رشد آن در قرن 17 با بوجود آمدن هندسه تحلیلی و حساب دیفرانسیل و انتگرال بود. اما در قرن 19 تجدید نظر کلی و پیشرفتهای فراوان در این علم بوجود آمد
نیکلای ایوانویچ لباچفسکی (Lobachevsky, Nikolay Ivanovich) از جمله اولین کسانی بود که قواعد هندسه اقلیدسی را که بیش از 2000 سال بر علوم مختلف ریاضی و فیزیک حاکم بود درهم شکست. کسی باورش نمی شد هنگامی که اروپا مرکز علم بود شخصی در گوشه ای از روسیه بتواند پایه های هندسه اقلیدسی را به لرزه در بیاورد و پایه های علم در قرن نوزدهم را پی ریزی کند.
خیال نداریم راجع به خود او صحبت کنیم بلکه می خواهیم بطور مختصر بیان کنیم که او چه کرد. در میان اصول هندسه اقلیدسی اصلی وجود دارد به اینصورت : از هر نقطه خارج یک خط نمی توان بیش از یک خط موازی ( در همان صفحه ای که خط و نقطه در آن قرار دارند) به موازات آن خط رسم کرد.
در طول سالها این اصل اقلیدس مشکل بزرگی برای ریاضی دانان بود. چرا که ظاهری شبیه به قضیه داشت تا اصل. مقایسه کنید آنرا با این اصل اقلیدس که می گوید بین هر دو نقطه می توان یک خط راست کشید و یا اینکه همه زوایای قائمه با هم برابر هستند.
حقیقت آن است که بسیاری از ریاضی دانان سعی کردند که این اصل اقلیدس را اثبات کنند اما متاسفانه هرگز این امر ممکن نشد. حتی خیام در برخی مقالات خود سعی در اثبات این اصل کرد اما او نیز همانند سایرین به نتیجه نرسید.
لباچفسکی (1792 - 1856) نیز همانند بسیاری از دانشمندان علوم ریاضی سعی در اثبات این اصل کرد و هنگامی که به نتیجه مطلوب نرسید نزد خود به این فکر فرو رفت که این چه هندسه ای است که بر پایه چنین اصل بی اعتباری استوار شده است. اما لباچفسکی در کوشش بعدی خود سعی کرد تا رابطه میان هندسه و دنیای واقعی را پیدا کند.
او معتقد بود اگر نتوانیم از سایر اصول هندسه اقلیدسی این اصل را ثابت کنیم باید به فکر مجموعه اصول دیگری برای هندسه باشیم. اصولی که در دنیای واقعی حضور دارند. او پس از بررسی های بسیار چنین بیان کرد :
از هر نقطه خارج یک خط می توان لااقل دو خط در همان صفحه به موازات خط رسم کرد
هر چند پس از این فرض بنظر می رسید که وی در ادامه به تناقض های بسیاری خواهد رسید اما او توانست بر اساس همین فرض و مفروضات قبلی اقلیدس به مجموعه جدید از اصول هندسی برسد که حاوی هیچگونه تناقضی نباشد. او پایه های هندسه ای را بنا نهاد که بعدها کمک بسیار زیادی به فیزیک و مکانیک غیر نیوتنی نمود
در کشور ما ایران در سده های چهارم و پنجم هجری ، بسیاری از ریاضی دانان ایرانی ، به بررسی تصاعد ها پرداخته اند از جمله « ابوریحان بیرونی » در کتاب خود به نام « آثار الباقیه عن القرون الخالیه » مسئله معروف صفحه شطرنج را که در واقع مسئله ای مربوط به یک تصاعد هندسی است که جمله ی اول آن واحد و تعداد جمله ها 64 باشد ، حل کرده است و با استدلال دقیق ، مجموع جمله های این تصاعد را به دست آورده است
18446744073551615.
درباره صفحه شطرنج ، روایتی وجود دارد . وقتی مخترع شطرنج ، کشف خود را به شاه عرضه کرد ، شاه از اوخواست پاداشی بخواهد ، دانشمند پاسخ داد : به خاطر خانه اول شطرنج ، یک دانه گندم به من بدهید و به خاطر خانه دوم دو دانهی گندم و به خاطر خانه سوم چهار دانهی گندم و همینطور برای هر خانه دو برابر خانهی پیش از آن گندم به من بدهید تا به خانه شصت و چهارم برسد . شاه با ساده لوحی فرمان داد یک کیسه گندم به این مرد بدهید . ولی او نپذیرفت و تقاضا کرد پس از محاسبه دقیق ، گندم را به او بدهند و پس از محاسبه، عددی را که در بالا آوردیم پیدا شد .که اگردر تمام سطح کره زمین (یعنی هر جا که خشکی باشد ) گندم بکارند این مقذار گندم به دست نمی آید. ابوریحان بیرونی با استدلال به این نتیجه رسید که مقدار گندم ها برابر 264-1 و برای محسوس کردن این عدد می گوید:در سطح کره مین 2305 کوه را در نظر می گیریم ، اگر از هر کوه 10000رود جاری شود ، در طول رود خانه 1000قطار قاطر حرکت کند و هرقطار شامل 1000قاطر باشد و بر هر قاطر 8 کیسه گندم قرار داده باشیم . ودر هر کیسه 10000دانه گندم باشد . آن وقت عدد همهی این گندم ها از تعداد گندم های صفحه شطرنج کوچکترمی شود.
+ نوشته شده در شنبه بیست و هشتم آبان ۱۳۹۰ ساعت 18:22 توسط نیلو
|

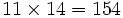
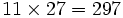
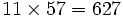
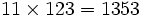
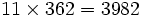

























 جوهر ریاضی درآزادی آن نهفته است.
جوهر ریاضی درآزادی آن نهفته است.